Question

1. BBQ sells over 200 products. Product A has sales of 400,000 units per year. The carry cost of each product is $36. The order cost is $28. a. How much is the optimum order quantity? b. How frequently should they reorder in days? 2. You were asked to examine the inventory policy for the company you work for. You start with its most popular product line. The carry cost for the product is $15 per unit and the reorder cost regardless of the number of units ordered is $40. It sells 75,000 units a year. Its current inventory policy is to reorder 700 units each time the inventory goes to zero. a. Is this a good policy? b. If not why not? c. What do you recommend?

Answer 1

a) The optimum order quantity is 789 units per order.

b) They have to reorder every 0.72 days.

2)

a) It is not a good policy.

b) The quantity per order is greater than the optimum quantity per order.

c) The order quantity should be 632 units/order

Step-by-step explanation:

The carry costs are the costs incurred by the company for having the products in stock (financial, storage, etc). They are proportional to the average inventory held by the company.

The order costs are the costs associated with the purchase order. They are proportional to the amounts of purchase orders by unit of time.

a) The optimum order quantity can be calculated with the Economic Order Quantity (EOQ) formula. This formula minimizes the sum of the carry costs and the order costs.

In this formula:

EOQ: Economic Order Quantity or optimum order quantity

S: Order costs

D: Annual quantity demanded

H: Carry cost

`EOQ =\sqrt{(2SD)/(H) }=\sqrt{(2*28*400,000)/(36) }= √(622,222.22) =788.81 \approx 789`

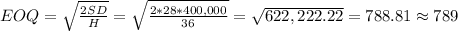
The optimum order quantity is 789 units per order.

b) If the annual demand is 400,000 and the quantity per order is 789 units, the company will do 506.97 orders a year.

`(400,000\,units/year)/(789 \,units/order)= 506.97 \,orders/year`

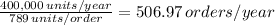
If we take 365 days a year, we have 1.39 orders a day.

`506.97(orders)/(year)*(1\,year)/(365\,days)=  1.39 orders/day`

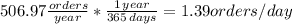
This means it has to reorder every 0.72 days.

2) If we apply the EOQ formula we get:

`EOQ=\sqrt{(2SD)/(H) }= \sqrt{(2*40*75,000)/(15) }= √(400,000)= 632.45`

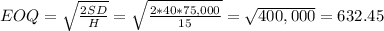
a) It is not a good policy.

b) The quantity per order is greater than the optimum quantity per order.

c) The order quantity should be 632 units/order