Question

General equation+ solution pls

Answer 1

82/5cm

Explanation:

((x + 4) + x)(2x - 1) - (x + 4)

(x + 4)^2 + --------------------------------- = 783

2

(2x + 4)(2x - 1) - (x + 4)

x^2 + 8x + 16 + ------------------------------ = 783

2

x^2 + 8x + 16 + (4x^2 + 6x - 4) - (x + 4) = 783 • 2

5x^2 + 13x + 8 = 1566

5x^2 + 13x - 1558 = 0

(5x - 82)(x + 19) = 0

x = 82/5 (legible coz measurements are positive value)

or -19(illegible coz there are no negative value in measurements)

Answer 2

x = 18.5 cm

Explanation:

We are given the expression as well as value of the area of the shape, and therefore we can equate these two:

`(x+4)^2 + (((x+4) + x)((2x-1) - (x+4)))/(2) = 783`

Now, in order to find the value of
`x`, we have to make it the subject:

Expanding brackets and simplifying:

⇒
`x^2 + 8x + 16 + ((2x + 4)(2x - 1 - x - 4))/(2) = 783`

⇒
`x^2 + 8x + 16 + ((2x+4)(x - 5))/(2) = 783`

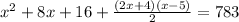
Multiplying the brackets on the top part of the fraction and simplifying:

⇒
`x^2 + 8x + 16 + (2x^2 - 10x + 4x - 20)/(2) = 783`

⇒
`x^2 + 8x + 16 + (2x^2 - 6x - 20)/(2) = 783`

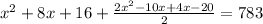
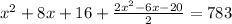
We can remove the denominator from the fraction by dividing the top part of the fraction by 2:

⇒
`x^2 + 8x + 16 +{x^2 - 3x - 10} = 783`

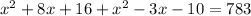
Now we can collect like terms together:

⇒
`2x^2 + 5x + 6 = 783`

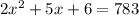
Subtract 783 from both sides:
⇒
`2x^2 + 5x + 6 - 783 = 0`

⇒
`2x^2 + 5x -777 = 0`

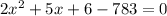
Finally, we can use the quadratic formula to find the value of
`x`:

`\boxed{x = (-b \pm √(b^2 - 4ac))/(2a)}`,

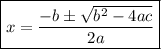where:

a = 2

b = 5

c = -777.

∴
`x = (-5 \pm √(5^2 - 4(2)(-777)))/(2(2))`

⇒
`x = (-5 \pm √(25 - (-6216)))/(2(2))`

⇒
`x = (-5 \pm √(6241))/(4)`

⇒
`x = (-5 \pm 79)/(4)`

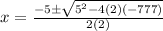
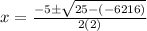
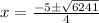
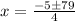
We have to use the positive value of
`x` because length cannot be a negative number:

⇒
`x = (-5 + 79)/(4)`

⇒
`x = (74)/(4)`

⇒
`x = \bf 18.5`

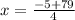
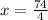
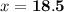
∴ The length of the side represented by
`x` is 18.5 cm.