Question

An apple orchard has an average yield of 40 bushels of apples per tree if tree density is 28 trees per acre. For each unit increase (decrease) in tree density, the yield decreases (increases) by 2 bushels per tree. How many trees per acre should be planted to maximize the yield?

Answer 1

24 trees per acre

Explanation:

Let x be the optimal tree density per acre and y be the number of bushels yield per tree

Since for each unit change of x from 28 trees/acre, we have 2 unit change of y from 40 bushels per tree in the reversed direction

Change of x from 28 is x - 28

Change of y from 40 is y - 40

Therefore we have y - 40 = -2(x - 28) or y = 40 - 2(x - 28) = -2x + 96

The total bushels per acre should be y bushels/tree * x tree/acre. We want to optimize this. Substitute the above equation in for y and we have

`T = xy = x(-2x+96)`

`T = -2x^2 + 96x`

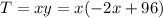
To find the maximum value of this, we can take the first derivative and set it to 0

`T^(') = -4x + 96 = 0`

`4x = 96`

`x = 24`

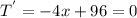
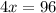
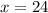
We know this is a maxima because
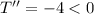`T{''} = -4 < 0`. So T is maximum when x = 24 trees per acre