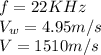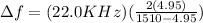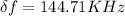Question

The sound source of a ship’s sonar system operates at a frequency of 22.0 kHz. The speed of the sound wave emitted by the source in sea water is 1510 m/s. What is the difference in frequency between the directly radiated waves and the waves reflected from a whale traveling directly toward the ship at 4.95 m/s

Answer 1

`\Delta f= 144.71KHz`

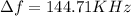
Step-by-step explanation:

We define two formulas. Firt for the stationary object and then for the shpo,

The frequency formula for the stationary is,

`f_(Lr)=(V+V_w)/(V)f^1\\f_(S)=(V)/(V-V_w)f^2`

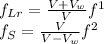
We need to find the difference or the rate of the relevant frequencies, that is

`\Delta f= f_(Lr)-f_S\\\Delta=f(2V_w)/(V-V_w)`

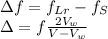
With the dates that we have, we only make a substitution,

`f=22 KHz\\V_w = 4.95m/s\\V= 1510m/s`

`\Delta f= (22.0KHz)((2(4.95))/(1510-4.95))`

`\delta f= 144.71KHz`