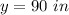Answer:
Part a)
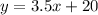
Part b)
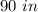
Explanation:
Part a) Create a linear equation to represent this situation
Let
x -----> the number of years
y ----> the height in inches
we have the points
(020) ----> at birth the height was 20 inches
(8,48) ---> 8th birthday the height was 48 inches
step 1
Find the linear equation in slope intercept form

where
m is the slope
b is the y-coordinate of the y-intercept
Find the slope m
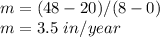
Find the value of b
 ----> the point (0,20) is the y-intercept
----> the point (0,20) is the y-intercept
substitute
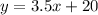
Part b) According to your equation, how tall will you be at age 20?
For x=20 years
substitute the value of x in the linear equation and solve for y