Question

A loop of wire is placed in a magnetic field such that it has a flux, LaTeX: \phi ϕ, through it. The loop is compressed so that the area is reduced to 0.3 its original value while not changing the orientation of the loop with the magnetic field. If the flux is to remain the same, by what factor must the magnetic field change? Answer to one decimal place.

Answer 1

3.33

Step-by-step explanation:

We are given that

Magnetic flux of loop of wire=
`\phi`

Let original area of loop of wire=A

Initial magnetic field produced in wire= B

We have to find the change in magnetic when area is reduced by 0.3 its original value.

We know that magnetic flux

`\phi=BAcos\theta`

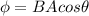
When area is reduced by 0.3

`A'=0.3 A`

`\phi'=0.3 B'A cos\theta`

`\phi'=\phi`

`0.3 B'A cos\theta= BA cos\theta`

`B'=(B)/(0.3)=3.33 B`

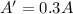
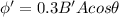
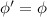
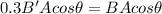
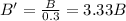
When area is reduced to 0.3 its original value then magnetic field is 3.33 times the initial value.Therefore, the magnetic field increases.

Answer 2

B'= 3.333 B

Step-by-step explanation:

Lets take

Initial area = A

Magnetic field = B

The area after compression

A'=0.3 A

Magnetic field = B'

We know that flux ,Ф

Ф = B A

Given that flux is constant so

B A = B' A'

B A=B' x 0.3 A

B'= 3.333 B

It means that magnetic field will increase.