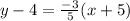Question

How to find point form of (-5,4) and (5,1)

Answer 1

The point slope form of (-5, 4) and (5, 1) is
`y-4=(-3)/(5)(x+5)`

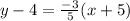
Solution:

Given that a line is passing through points (-5,4) and (5,1)

We need to determine point slope form of line

Equation of line passing through point
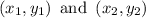`\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right)` is given as:

`\mathrm{y}-\mathrm{y}_(1)=\frac{\left(\mathrm{y}_(2)-\mathrm{y}_(1)\right)}{\left(\mathrm{x}_(2)-\mathrm{x}_(1)\right)}\left(\mathrm{x}-\mathrm{x}_(1)\right)`

`\text { In our case } x_(1)=-5, y_(1)=4, x_(2)=5, y_(2)=1`

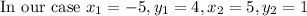
Substituting given value in (1) we get

`\begin{array}{l}{y-4=((1-4))/((5-(-5)))(x-(-5))} \\\\ {=>y-4=(-3)/(10)(x-(-5))} \\\\ {=>y-4=(-3)/(5)(x+5)}\end{array}`

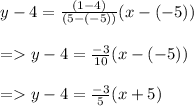
Hence the point slope form of line is
`y-4=(-3)/(5)(x+5)`