Final answer:
To find the approximate period of rotation of the Sun in days, we can use the fact that the Sun's rotation rate is 2 km/s. Using the equation v = 2πR/T, we can solve for the period T. Given that the Sun is located about 26,000 light-years from the center of the Galaxy, we can calculate the circumference of the Sun's orbit as 2πR = 162,920 light-years. Substituting the values into the equation for the period, we find T ≈ 3.5793 ×
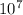 s.
s.
Step-by-step explanation:
To find the approximate period of rotation of the Sun in days, we can use the fact that the Sun's rotation rate is 2 km/s. We know that the difference in radial velocities of the east and west edges of the Sun is about 4 km/s. Since the Sun rotates in a circular motion, we can equate this difference in velocities to the tangential velocity of an object moving around a circle, which is given by v = 2πR/T (where v is the velocity, R is the radius, and T is the period). From this, we can solve for the period T, which gives us T = 2πR/v. Given that the speed of light is 300,000 km/s and the Sun is located about 26,000 light-years from the center of the Galaxy, we can calculate the circumference of the Sun's orbit as 2πR = 2π(26,000 light-years) = 162,920 light-years. Converting this to kilometers and using the fact that there are approximately 31,536,000 seconds in a year, we find that the circumference of the Sun's orbit is approximately 492,500,000,000 km. Now, we can substitute the values of R and v into the equation for the period to find T ≈ 2π(492,500,000,000 km)/(2 km/s) ≈ 3.0856 ×
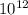 . Converting this to days, we have T ≈ 3.5793 ×
. Converting this to days, we have T ≈ 3.5793 ×
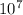 days.
days.