Question

A mass of 4kg stretches a spring 40cm. Suppose the mass is displaced an additional 12cm in the positive (downward) direction and then released. Suppose that the damping constant is 3 N⋅s/m and assume g=9.8m/s2 is the gravitational acceleration. (a) Set up a differential equation that describes this system. Let x t

Answer 1

A differential equation is
`4x''+3x'+98x=0`.

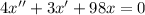Step-by-step explanation:

Given that,

Mass = 4 kg

Stretch string = 40 cm

Additional distance = 12 cm

Damping constant = 3 N-s/m

Let xx to denote the displacement, in meters, of the mass from its equilibrium position, and give your answer in terms of x,x′,x′′ .

We need to calculate the spring constant k

The net force in y direction at equilibrium position

`F_(y)=0`

`mg-kx=0`

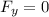
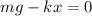
Put the value into the formula

`4*9.8-k*40*10^(-2)=0`

`k=(4*9.8)/(40*10^(-2))`

`k=98\ N/m`

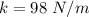
The initial displacement from equilibrium

`x(0)=12\ cm`

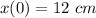
The initial velocity is

`v(0)=0`

We need to set up a differential equation

The net force in y direction is zero at equilibrium position .

`\Sum F_(y)=0`

`mx''+cx'+kx=0`

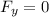
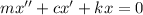
Put the value into the equation

`4x''+3x'+98x=0`

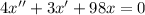
Hence, A differential equation is
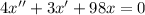`4x''+3x'+98x=0`.