Question

The cost for a carton of milk is $3, and it is sold for $5. When the milk expires, it is thrown out. You also know that the mean of historical monthly demand is 1,500 and the standard deviation is 200.

a.What is the cost of overstocking and understocking?
b.Calculate the critical ratio.
c.What is the optimal quantity of milk cartons that should be

Answer 1

a) $3

b) $2

c) 1449

Step-by-step explanation:

Given:

The cost for a carton of milk = $3

Selling price for a carton of milk = $5

Salvage value = $0 [since When the milk expires, it is thrown out ]3

Mean of historical monthly demand = 1,500

Standard deviation = 200

Now,

a) cost of overstocking = Cost for a carton of milk - Salvage value

= $3 - $0

= $3

cost of under-stocking = Selling price - cost for a carton of milk

= $5 - $3

= $2

b) critical ratio =
`\frac{\textup{cost of under-stocking }}{\textup{cost of overstocking + cost of under-stocking }}`

or

critical ratio =
`\frac{\textup{2}}{\textup{3 + 2}}`

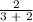
or

critical ratio = 0.4

c) optimal quantity of milk cartons = Mean + ( z × standard deviation )

here, z is the z-score for the critical ration of 0.4

we know

z-score(0.4) = -0.253

thus,

optimal quantity of milk cartons = 1,500 + ( -0.253 × 200 )

= 1500 - 50.6

= 1449.4 ≈ 1449 units