Answer:
Density of propane = 17.8 g/L
Propane is more priced than gasoline
Step-by-step explanation:
Given:
Temperature, T = 298 K
Pressure, P = 10 bar = 0.987 × 10 = 9.87 atm
now,
Molar mass of propane, M = 44.1 g/mol
From ideal gas law
⇒ PV = nRT
here,
n is the number of moles
R is the ideal gas constant = 0.0821 L.atm/mol.K
also,
Density, D =
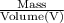
or
V =
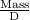
and,
nM = mass
thus,
V =
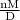
substituting in the ideal gas relation
we have
P =
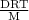
or
D =

or
D =

or
D = 17.8 g/L
Now,
1 gallon = 3.78 Liter
Therefore,
5 gallon = 5 × 3.78 Liter = 18.9 Liter
Thus,
mass of 5 gallon propane = Volume × Density
= 18.9 Liter × 17.8 g/L
= 336.42 g
or
= 0.336 kg
also it is given that Price of 5 gallon propane i.e 0.336 kg = $30
Therefore,
Price per kg =
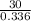
= $89.28
and,
Mass of 5 gallons i.e 18.9 Liter gasoline = Density × Volume
= 0.692 g/cm³ × 18.9 Liter
also,
1 L = 1000 cm³
thus,
= 0.692 g/cm³ × 18.9 × 1000 cm³
= 13078.8 g
or
= 13.078 kg
Therefore,
Price per kg of gasoline =
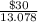
= $2.29
hence, propane is more priced than gasoline