Question

If a ball is thrown vertically upward with a velocity of 80 ft/s, then its height after ???? seconds is ????(????)=80????−16????2. (a) What is the maximum height reached by the ball? (b) What is the velocity of the ball when it is 96 ft above the ground on its way up? (c) What is the velocity of the ball when it is 96 ft above the ground on its way down?If a ball is thrown vertically upward with a velocity of 80 ft/s, then its height after ???? seconds is ????(????)=80????−16????2. (a) What is the maximum height reached by the ball? (b) What is the velocity of the ball when it is 96 ft above the ground on its way up? (c) What is the velocity of the ball when it is 96 ft above the ground on its way down?

Answer 1

100 ft

16 ft/s

16 ft/s

Step-by-step explanation:

t = Time taken

u = Initial velocity

v = Final velocity

s = Displacement

a = Acceleration due to gravity = 32 ft/s² (negative upwards and positive downwards)

The function here is of the form which is one of the equations of motion

`s=ut+(1)/(2)at^2\\\Rightarrow s=80t+(1)/(2)32t^2\\\Rightarrow s=80t+16t^2`

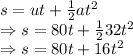
From another equation of motion

`v^2-u^2=2as\\\Rightarrow s=(v^2-u^2)/(2a)\\\Rightarrow s=(0^2-80^2)/(2* -32)\\\Rightarrow s=100\ ft`

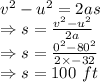
The maximum height the ball will reach is 100 ft

When s = 96 ft

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* -32* 96+80^2)\\\Rightarrow v=16\ ft/s`

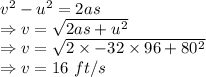
The velocity of the ball when it is 96 ft above the ground on its way up is 16 ft/s

On the way down when it will be 96 ft above the ground it would travel 100-96 = 4 ft from the maximum height

`v^2-u^2=2as\\\Rightarrow v=√(2as+u^2)\\\Rightarrow v=√(2* 32* 4+0^2)\\\Rightarrow v=16\ ft/s`

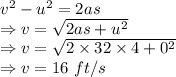
The velocity of the ball on the way down when it is 96 ft above the ground is 16 ft/s