Answer:
I = 188.5 Kg m²
Step-by-step explanation:
The moment of inertia of your body is given by the relationship
I = ∫ r² dm
Since the mass and the squared distance are scalars the moment of inertia is additive, we just have to take into account from where they are measured.
In addition, we will use the parallel axes theorem, there is the moment of inertia for any axis to the center of mass, where we can consider mass as punctual
I =
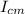 + M D²
+ M D²
Our body is formed by two bodies: the rod and the sphere. Suppose the system is on the x axis
-Moment of inertia the rod, with an axis at one end
as the bar is uniform let's define a longitudinal mass density
λ = m / L = dm / dx
dm = λ dx
I = ∫ x² (λ dx) = λ ∫ x² dx
I = λ x³/3
We evaluate from the lower limit x = 0 to the upper limit x = L
I = λ (L³/3 -0)
Let's change the density for its value
I = M/L L³ / 3
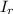 = M L² / 3
= M L² / 3
-Moment of inertia of the sphere with respect to an axis at the end of the rod
In this case we will use the moment of inertia of the center of mass and then use the parallel axes theorem
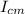 = 2/5
= 2/5
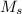 R²
R²
The distance is the length of the rod
D = L
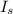 = 2/5
= 2/5
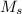 Rs2 +
Rs2 +
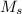 L2
L2
Total inertia element is the sum of these two
I =
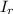 +
+
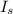
I =
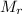 L² / 3 + 2/5
L² / 3 + 2/5
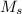
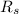 ² +
² +
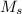 L²
L²
Let's replace and calculate
For our case
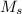 = 5
= 5
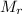
L = 4R
I =
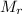 L² / 3 + 2/5 (5
L² / 3 + 2/5 (5
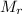 ) (L/4)² 2 + (5
) (L/4)² 2 + (5
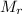 ) L²
) L²
I =
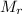 L² (1/3 + 1/8 + 5)
L² (1/3 + 1/8 + 5)
I =
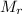 L² (5,458)
L² (5,458)
I = 6.59 5.24 5.458
I = 188.5 Kg m²