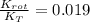Question

A bicycle has wheels of radius 0.320 m. Each wheel has a rotational inertia of 0.0800 kg⋅m2 about its axle. The total mass of the bicycle including the wheels and the rider is 55.0 kg. When coasting at constant speed, what fraction of the total kinetic energy of the bicycle (including rider) is the rotational kinetic energy of the wheels?

Answer 1

`\frac{K_(rot)} {K_T} = 0.019`

Step-by-step explanation:

We know that Rotational Kinetic Energy is given by,

`K_(rot)=(1)/(2)Iw^2`

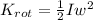
Where I is the inertia and w the angular velocity. We know as well that
`w= (v)/(r)`

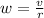
The we can replace,

`K_(rot) = (1)/(2)I((v)/(r))^2`

`K_(rot) = (1)/(2)I((v^2)/(r^2))`

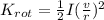
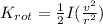
That equation are perfect for the 4 wheel, however we need a similar expresion for the ycycle

`K_(tran) = (1)/(2)mv^2`

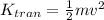
The total energy can be expressed as follow,

`K_T = K_(rot)+K{tran}`

`K_T=2((1)/(2)I(v^2)/(r^2))+(1)/(2)mv^2`

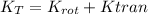
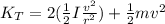
Whit this expression is easy to find te ratio of rotational kinetic energy, we need to make the relation between
`K_(rot) \Rightarrow K_T`

`\frac{K_(rot)} {K_T} = (2I)/(2I+mr^2)`(You only need to put the previous values and simplify)

Substituting
`I=0.08kg.m^2, m=79kg and r=0.32m`

We have

`\frac{K_(rot)} {K_T} = (2I)/(2I+mr^2) \\\frac{K_(rot)} {K_T} = (2(0.08))/(2(0.08)+(79)(32))`

`\frac{K_(rot)} {K_T} = 0.019`