Question

In a certain high school, 20% of the graduating seniors have chosen to attend The Ohio State University. If there are 265 seniors in the graduating class, the number who will go to The Ohio State University is a binominal random variable. What is the standard deviation of the number of students who will attend Ohio State?

Answer 1

Answer: 6.51

Explanation:

For x be a binomial variable with parameters n (number of trials ) and p (probability of getting success in each event)

The standard deviation is given by :-

`\sigma=√(np(1-p))`

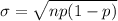
As per given , we have

Number of seniors in the graduating class : n= 265

The probability the graduating seniors have chosen to attend The Ohio State University : p=20%= 0.20

Now, the standard deviation of the number of students who will attend Ohio State :-

`\sigma=√(265(0.20)(1-0.20))\\\\=√(265(0.20)(0.80))=6.51152823844\approx6.51`

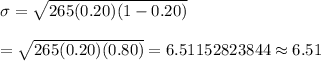
Hence, the standard deviation of the number of students who will attend Ohio State = 6.51