Answer:
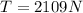
Step-by-step explanation:
The Young's modulus is defined as the quotient of the stress and the strain in a material. So
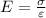
And, how does Young's modulus is related to the tension (in this particular case in the tendon)? We can use the definition of stress and strain:
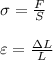 ,
,
Where F is the applied force to the material, S is the cross-sectional area of the material,
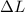 is the deformation and L is the original length.
is the deformation and L is the original length.
In this case
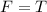 , so we can rewrite the Young's modulus expression as follows:
, so we can rewrite the Young's modulus expression as follows:
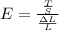 ,
,
now solving for T we get
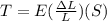 .
.
Before computing the tension we need to compute the cross-sectional area and the deformation.
The cross-sectional area is the cross section of a cylinder (the tendon's form):
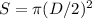 ,
,
where D is de diameter (
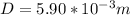 ).
).
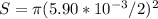 ,
,
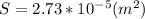 .
.
The Deformation is simply the change in length, so
 .
.
Now we can easily compute the tension:
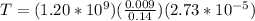 ,
,
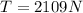 .
.