Question

The Super Discount store (open 24 hours a day, every day) sells 8-packs of paper towels, at the rate of approximately 420 packs per week. Because the towels are so bulky, the annual cost to carry them in inventory is estimated at $.50. The cost to place an order for more is $20 and it takes four days for an order to arrive.

a. Find the optimal order quantity.
b. What is the reorder point?
c. How often should an order be placed?

Answer 1

a) 2,093

b) It will reorder once there are 420 units left (demand during lead-time)

c) 34 days

Step-by-step explanation:

a) economic order quantity

`Q_(opt) = \sqrt{(2DS)/(H)}`

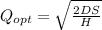
Where:

D = annual demand = 21,900

S= setup cost = ordering cost = 50

H= Holding Cost = 0.50

`Q_(opt) = \sqrt{(2(21,900)(50))/(0.50)}`

EOQ = 2092.844954

b) it takes four days to arrive:

if it sale 420 units per week then:

420 x 4/7 = 240 units are demand during delivery

c) order cycle:

EOQ / Annual Demand

2,093 / 21,900 = 0,09557 x 365 = 34.8333 days

It will order every 34 days (if it orders after 35 days will face shortage)