Answer:
Each Side of the squared deck = (w + 5)
If w = 4, the area of the square = 81 sq units
perimeter of the square = 36 units,
Explanation:
The area of the square deck is
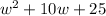
Now, Area of the Square is
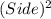
Factorizing the given expression, we get
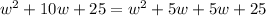
or,

or,
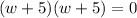
⇒

⇒ The area of the Square deck is
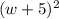
Comparing it with the formula for area,
we get each Side of the squared deck = (w + 5)
Now, if w = 4, then each side = 4+ 5 = 9 units
Hence, the area of the square = 9 x 9 = 81 sq units
Perimeter of the squire = 4 x SIDE = 4 x 9 = 36 units