Question

The area of a rectangle is x²+3x-18. Find the dimensions of the rectangle in terms of x.

Answer 1

The dimensions of the rectangle in terms of x are (x+6) and (x-3).

Explanation:

The area of the triangle = LENGTH X WIDTH

Now, here the given expression for area is
`x^(2)  + 3x   -18`

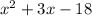
Factorize the given expression, we get

`x^(2)  + 3x   -18   = x^(2)  + 6x  -3x  -18`

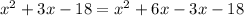
or,
`x^(2)  + 6x  -3x  -18  =  0`

⇒
`x(x+6)-3(x+6) =0`

⇒
`(x+6)(x-3) =0`

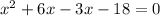
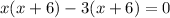
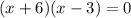
So, the given area expression
`x^(2)  + 3x   -18  = (x+6)(x-3)`

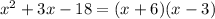
Hence, the dimensions of the rectangle are (x+6) and (x-3).