Question

There are 412 students and 20 teachers taking buses on a trip to a museum. Each bus can seat a maximum of 48. Which inequality gives the least number of buses, b, needed for the trip?

Answer 1

The inequality
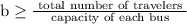`\mathrm{b} \geq \frac{\text { total number of travelers }}{\text { capacity of each bus }}` gives the least number of buses, b, needed for the trip. The least number of buses is 9

Solution:

Given that, There are 412 students and 20 teachers taking buses on a trip to a museum.

Each bus can seat a maximum of 48.

We have to find which inequality gives the least number of buses, b, needed for the trip?

Now, there are 412 students and 20 teachers, so in total there are 412 + 20 = 432 travelers

The number of buses required “b” is given as:

`\text { (b) } \geq \frac{\text { total number of travelers }}{\text { capacity of each bus }}`

`\text { So, number of buses required } \geq (432)/(48)`

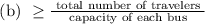
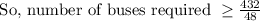
Number of buses required ≥ 9 buses.

But least number will be 9 from the above inequality.

Hence, the inequality
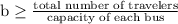`\mathrm{b} \geq \frac{\text {total number of travelers}}{\text {capacity of each bus}}` gives least count of busses and least count is 9.