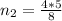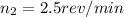Question

Two​ pulleys, one with radius 4 inches 4 inches and one with radius 8 inches 8 inches​, are connected by a belt. If the 4 dash inch4-inch pulley is caused to rotate at 5 revolutions per minute5 revolutions per minute​, determine the revolutions per minute of the 8 dash inch8-inch pulley. ​ (Hint: The linear speeds of the pulleys are the​ same, both equal the speed of the​ belt.)

Answer 1

`n_2 = 2.5 rev/min`

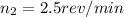
Step-by-step explanation:

The pulleys are two wheels, one driving, which is where the motor is that makes it spin, and another driven thanks to the friction that occurs between them and a belt that joins them. It is evident, seeing this example, that the smallest wheel should turn faster than the largest.

In all pulleys the formula is met:

`n_1 * D_1 = n_2* D_2`

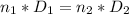
where "D1" and "D2" is the value of the diameter (or ratio)of each of the pulleys and "n1" and "n2" is the speed of rotation, that is, the number of revolutions per minute given by each pulley.

So

`D_1 = 4in\\D_2 = 8in\\n_1 = 5rev/min\\n_2=?`

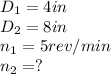
Replacing,

`(4)(5)=n_2(8)`

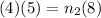
clearing n_2

`n_2 = (4*5)/(8)`

`n_2 = 2.5 rev/min`