Question

The base of a rectangular box is to be twice as long as it is wide. The volume of the box is 108 cubic inches. The material for the top costs $0.50 per square inch and the material for the sides and bottom costs $0.25 per square inch. Find the dimensions that will make the cost a minimum.

Answer 1

Step-by-step explanation:

First we express teh other sides as expression of b (wide)

being the volume: a x b x c

and the base: a x b

if the base is long as wide then:

a = 2b

so we can construct:

2b x b x c = 2b^2 x c = 108

and we clear c:

c = 108/ (2b^2) = 54/b^2

Now we construct the cost formula:

ab x 0.50 (cost for the top part)

now the cost of the sides (there are four) and the bottom part:

(2bc + 2ac + ab) x 0.25

total cost: ab x 0.50 + (2bc + 2ac + ab) x 0.25

we replace a and c as expression of b:

`(2b)b * 0.50 + (2b(54)/(b^2) + 2(2b)(54)/(b^2) + (2b)b) * 0.25`

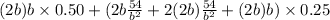
and now we solve for b:

`b^2 + ((108)/(b) + (216)/(b) + 2b^2) * 0.25`

`b^2 + (81)/(b) + (b^2)/(2)`

`(1.5)b^2 + (81)/(b)`

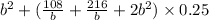
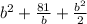
Now we derivate the cost function: (considering)

`a^(x)  = xa\\(1)/(a^(x)) = -(1x)/(a^(x+1))`

3b - 81/b^2 = 0

3b^3 = 81

b^3 = 81/3 = 27

b = third root of 27 = 3

now we solve for a:

a = 2b = 2(3) = 6

and last for c:

54/b^2 = 54/(3)^2 = 54/9 = 6

we check if we match the cubic inches:

a x b x c = 108

6 x 3 x 6 = 108