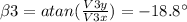Question

Several large firecrackers are inserted into the holes of a bowling ball, and the 6.4 kg ball is then launched into the air with a speed of 10.2 m/s at an angle of 35° from the horizontal. The firecrackers explode at the peak of the trajectory, breaking the ball into three pieces. A 1.4 kg piece travels straight back horizontally with a speed of 3.7 m/s. A 1.8 kg piece travels straight up with a speed of 11.1 m/s.

a. What is the magnitude of the velocity of the third piece?
b. What is the direction, θ, of the third piece

Answer 1

a. V3 = 19.36m/s

b. β3 = -18.8°

Step-by-step explanation:

Our given data is:

mt = 6.4kg; Vo = [10.2*cos(35°), 10.2*sin(35°)] m/s

m1 = 1.4kg; V1 = [-3.7, 0] m/s

m2 = 1.8kg; V2 = [0, 11.1] m/s

By inspection:

m3 = 3.2kg V3 = [ V3x, V3y]

At the point where the ball explodes, there's only x-component of the velocity, so:

Pix = Pfx and Piy = Pfy

On x-axis:

mt * Vo*cos(35°) = m1 * V1x + m3 * V3x

Solving for V3x:

V3x = 18.33 m/s

On y-axis:

0 = m2 * V2y + m3 * V3y

Solving for V3y:

V3y = -6.24 m/s

Therefore, the magnitude is:

`V3 = √(V3x^2 + V3y^2) = 19.36m/s`

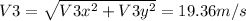
The angle is:

`\beta 3 = atan((V3y)/(V3x)) = -18.8\°`