Question

Father can paint the fence of their garden in 2 hours working alone. His son, alone, can paint the fence in 3.5 hours. How long will it take them to paint the fence together?

Answer 1

Father and son will paint a fence together in 1.2727 hours

Solution:

Given that

Number of hours taken by Father to paint a fence alone = 2 hours

Number of hours taken by Son to paint a same fence alone = 3.5 hours

Need to determine how much hours will be taken to paint the same fence when both father and son work together.

Let assume the work of painting the fence is represented by "x"

Work done by father alone in 2 hours = x

Work done by father alone in 1 hour =
`(x)/(2)`

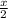
Work done by son alone in 3.5 hours = x

Work done by son alone in 1 hour =
`(x)/(3.5)`

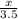
work done in 1 hour by father and son together = Work done by father alone in 1 hour + Work done by son alone in 1 hour

`\begin{array}{l}{=(x)/(2)+(x)/(3.5)=(x)/(2)+(2 x)/(7)} \\\\ {=(7 x+4 x)/(14)=(11 x)/(14)}\end{array}`

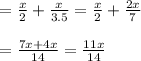
Number of hours required when working together is given as:

`=\frac{\text { Total Work }}{\text { work done together in } 1 \mathrm{hrs}}`

`=(x)/(\left((11 x)/(14)\right))=(14)/(11)=1.2727`

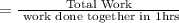
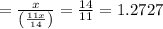
Hence father and son working together will paint a fence in 1.2727 hours.