Question

HELP!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!!! ANSWER ALL THREE OF THESE

Answer 1

`54°`

`38° = m∠LNM; 52° = m∠M`

`52° = m∠A`

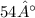
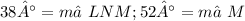
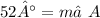
Explanation:

Use the Triangular Interior Angles Theorem to figure Part A out:

180° = 22° + x° + 104°

180° = 126° + x°

-126° - 126°

___________

54° = x

_______________________________________________

The measure of ∠C and the exterior angle measure of 105° sums up 180°, according to the Linear Pair Theorem:

180° = 105° +
`m∠C`

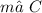
-105° - 105°

______________

`75° = m∠C`

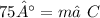
Then use the Triangular Interior Angles Theorem to figure out the
`m∠A`:

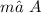180° = 53° + 75° +
`m∠A`

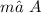
180° = 128° +
`m∠A`

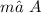
-128° - 128°

______________

`52° = m∠A`

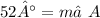
OR, you can use the Exterior Angles Theorem, which states that the exterior angle is opposite the side with two interior angles, so you would deduct the first interior angle from the exterior angle to get the measure of the second interior angle. In this case, you would deduct 53° from 105° to get 52°:

142° = 53° + m∠A

- 90° - 90°

_______________

`52° = m∠A`

_______________________________________________

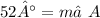
The measure of ∠N and the exterior angle measure of 142° sums up 180°, according to the Linear Pair Theorem:

180° = 142° +
`m∠N`

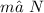
- 142° - 142°

______________

`38° = m∠N`

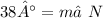
Then use the Triangular Interior Angles Theorem to figure out the
`m∠M`:

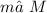180° = 38° + 90° +
`m∠M`

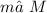
180° = 128° +
`m∠M`

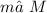
- 128° - 128°

______________

`52° = m∠M`

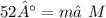
OR, you can use the Exterior Angles Theorem, which states that the exterior angle is opposite the side with two interior angles, so you would deduct the first interior angle from the exterior angle to get the measure of the second interior angle. In this case, you would deduct 90° from 142° to get 52°:

142° = 90° + m∠M

- 90° - 90°

_______________

`52° = m∠M`

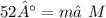
I am joyous to assist you anytime.