Question

An electron emitted in the beta decay of bismuth-210 has a mean kinetic energy of 390 keV. (a) Find the de Broglie wavelength of the electron. (b) Would such an electron be useful in a Davisson-Germer type scattering experiment? Address this question by determining the angle at which a first-order diffraction maximum would be found using the same nickel target as Davisson and Germ

Answer 1

Step-by-step explanation:

Given that,

The mean kinetic energy of the emitted electron,
`E=390\ keV=390* 10^3\ eV`

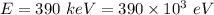
(a) The relation between the kinetic energy and the De Broglie wavelength is given by :

`\lambda=(h)/(√(2meE))`

`\lambda=\frac{6.63* 10^(-34)}{\sqrt{2* 9.1* 10^(-31)* 1.6* 10^(-19)* 390* 10^3}}`

`\lambda=1.96* 10^(-12)\ m`

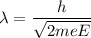
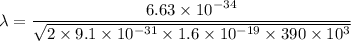
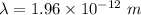
(b) According to Bragg's law,

`n\lambda=2d\ sin\theta`

n = 1

For nickel,
`d=0.092* 10^(-9)\ m`

`\theta=sin^(-1)((\lambda)/(2d))`

`\theta=sin^(-1)((1.96* 10^(-12))/(2* 0.092* 10^(-9)))`

`\theta=0.010^(\circ)`

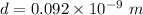
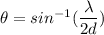
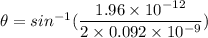
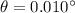
As the angle made is very small, so such an electron is not useful in a Davisson-Germer type scattering experiment.