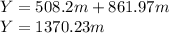Question

A rocket is launched at an angle of 39◦ above the horizontal with an initial speed of 90 m/s. It moves for 7 s along its initial line of motion with an acceleration of 19 m/s 2 . At this time its engines fail and the rocket proceeds to move as a projectile. The acceleration of gravity is 9.8 m/s 2 . Find the maximum altitude reached by the rocket. Answer in units of m.

Answer 1

Y=1370.23m

Step-by-step explanation:

The motion have two moments the first one the time the initial velocity is accelerating then when the engines proceeds to move as a projectile

`a=19 (m)/(s^(2) ) \\voy=vo*sin(\alpha )\\voy=90*sin(39 )\\y_(o)=0m\\y_(f)=y_(o)+v_(oy)*t+(1)/(2)*a*t^(2)\\y_(f)=90*sin(39)*7s+(1)/(2)*19(m)/(s^(2) )*(7)^(2)\\y_(f)=861.97m`

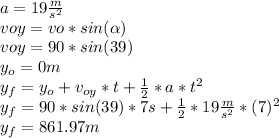
Now the motion the rocket moves as a projectile so:

`v_(fy)=v_(iy)+a*t\\v_(fy)=90+9.8*7\\v_(fy)=158.6 sin(39)`

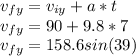
Now the final velocity is the initial in the second one

`v_(fy)^(2)=v_(fi)^(2)+2*a*yf \\\\a=g\\`

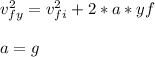
The maximum altitude Vf=0

`0=v_(fi)^(2)+2*a*yf \\\\yf=((158.6 sin(39))^(2) )/(2*9.8(m)/(s^(2) ) ) \\yf=508.26m`

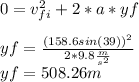
So total altitude is both altitude of the motion so:

`Y=508.2m+861.97m\\Y=1370.23m`