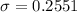Answer: 0.2551
Explanation:
Given : The temperature reading from a thermocouple placed in a constant-temperature medium is normally distributed with mean μ, the actual temperature of the medium, and standard deviation σ.
Significance level :

The critical z-value for 95% confidence :
 (1)
(1)
Since ,
 (where x be any random variable that represents the temperature reading from a thermocouple.)
(where x be any random variable that represents the temperature reading from a thermocouple.)
Then, from (1)
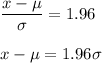 (2)
(2)
Also, all readings are within 0.5° of μ,
i.e.
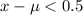
i.e.
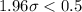 [From (2)]
[From (2)]
i.e.
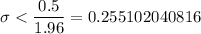
i.e.
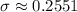
The required standard deviation :