The approximate distance between the docks is 356.59 feet approximately.
Solution:
Given, A boat is 400 feet away from one dock and 500 feet away from another dock.
The angle between the two paths is 45°.
Now, Let d be the distance between the docks, which forms a third leg of a triangle for which the angle opposite it has measure 45 degrees.
The other two legs have lengths 400 ft and 500 ft.
So, let us use the law of cosines:
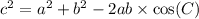
where a, b, c are sides of triangle and C is angle opposite to side c.
Here in our problem, c = d, a = 400, b = 500 and C = 45

Hence, the distance between two docks is 356.59 feet approximately.