Answer: 37
Explanation:
As per given description in the question, we have
Population standard deviation :
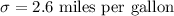
Critical value for 98% confidence interval =
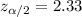
Margin of error : E= 1 mile per gallon
Formula we use to find the sample size :
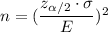
i.e.

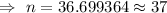
Therefore , the number of automobiles should be used in the test =37