Question

New Products pays no dividend at the present time. Starting in Year 3, the firm will pay a $0.25 dividend per share for two years. After that, the company plans on paying a constant $0.75 a share annual dividend indefinitely. How much should you pay per share to purchase this stock today at a required return of 13 percent?

Answer 1

You should pay $3.86 to purchase this stock.

Step-by-step explanation:

Hi, first let me mention that we can find the price of a stock by bringing to present value its future cash flows, in this case, its dividends, therefore we need to bring to present value $0.25 of year 3 and $0.25 of year 4. We also have to bring that constant dividend of $0.75 that the company plans to pay indefinitely, that we can do by using the following formula, discounted at 13%.

`PV(4)=(Constant Dividend)/(Discount Rate)`

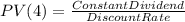
Notice that the formula above says PV(4), that is because this formula only brings that perpetual annuity to one period of time before the first payment takes place, therefore this value has to be brought to present value too.

With all the considerations above, this is how everything should look like.

`Price=(0.25)/((1+0.13)^(3) ) +(0.25)/((1+0.13)^(4) ) +(0.75)/(0.13) *(1)/((1+0.13)^(4) )`

`Price=0.17+0.15+3.54=3.86`

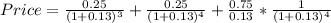
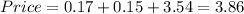
Therefore, the price of this stock is $3.86

Best of luck.