Question

Even though most corporate bonds in the United States make coupon payments semiannually, bonds issued elsewhere often have annual coupon payments. Suppose a German company issues a bond with a par value of €1,000, 20 years to maturity, and a coupon rate of 7.8 percent paid annually. If the yield to maturity is 8.9 percent, what is the current price of the bond? (Do not round intermediate calculations and round your answer to 2 decimal places, e.g., 32.16.)

Answer 1

The current price of the bond would be € 898.87

Step-by-step explanation:

Hi, we need to bring to present value the coupon payments and also the face value of the coupon in order to find the price of this bond, that can be done by using the following formula.

`Price=(Coupon((1+Yield)^(n)-1) )/(Yield(1+Yield)^(n) ) +(FaceValue)/((1+Yield)^(n) )`

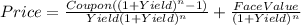
Where:

Coupon = 1,000*0.078=78

Yield = 0.089 (or 8.9%)

Face Value= 1,000

n = 20 coupon payments

So, everything should look like this.

`Price=(78((1+0.089)^(20)-1) )/(0.089(1+0.089)^(20) ) +(1,000)/((1+0.089)^(20) )`

`Price=717.13+181.74=898.87`

Therefore, the price of this bond is € 898.87

Best of luck.