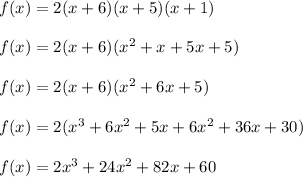Question

Write the cubic polynomial function f(x)in expanded form with zeros −6,−5,and −1, given that f(0)=60

f(x) =

Answer 1

`f(x)=2x^(3)+24x^(2)+82x+60`

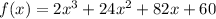
Explanation:

we know that

The roots of the polynomial are the values of x when the value of the polynomial f(x) is equal to zero

The roots of the polynomial function are

x=-6 -----> (x+6)=0

x=-5 -----> (x+5)=0

x=-1 -----> (x+1)=0

The equation of the cubic polynomial is

`f(x)=a(x+6)(x+5)(x+1)`

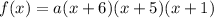
where

a is the leading coefficient

Remember that

f(0)=60

That means ------> For x=0 the value of f(x) is equal to 60

substitute the value of x and the value of y in the function and solve for a

`60=a(0+6)(0+5)(0+1)`

`60=a(6)(5)(1)`

`60=30a`

`a=2`

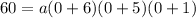
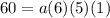
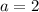
so

`f(x)=2(x+6)(x+5)(x+1)`

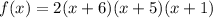
Applying the distributive property

Convert to expanded form

`f(x)=2(x+6)(x+5)(x+1)\\\\f(x)=2(x+6)(x^(2)+x+5x+5)\\\\f(x)=2(x+6)(x^(2)+6x+5)\\\\f(x)=2(x^(3)+6x^(2)+5x+6x^(2)+36x+30)\\\\f(x)=2x^(3)+24x^(2)+82x+60`