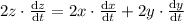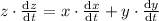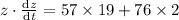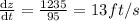Question

A balloon is rising vertically above a​ level, straight road at a constant rate of 2 ft divided by sec. Just when the balloon is 70 ft above the​ ground, a bicycle moving at a constant rate of 19 ft divided by sec passes under it. How fast is the distance s (t )between the bicycle and balloon increasing 3 seconds​ later?

Answer 1

Answer:13 ft/s

Step-by-step explanation:

Given

Balloon velocity is 2 ft/s upwards

Distance between balloon and cyclist is 70 ft

Velocity of cyclist is 19 ft/s

After 3 sec

cyclist traveled a distance of
`d_c=19* 3=57 ft`

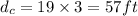
Distance traveled by balloon in 3 s

`d_b=2* 3=6 ft`

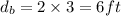
net height of balloon from ground =6+70=76 ft[/tex]

at
`t=3 s`

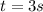
distance between cyclist and balloon is
`z=√(76^2+57^2)`

`z=95 ft`

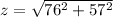
now suppose at any time t cyclist cover a distance of x m and balloon is at a height of h m

thus
`z^2=x^2+y^2`

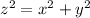
differentiating w.r.t time

`2 z\cdot \frac{\mathrm{d} z}{\mathrm{d} t}=2 x\cdot \frac{\mathrm{d} x}{\mathrm{d} t}+2 y\cdot \frac{\mathrm{d} y}{\mathrm{d} t}`

`z\cdot \frac{\mathrm{d} z}{\mathrm{d} t}=x\cdot \frac{\mathrm{d} x}{\mathrm{d} t}+ y\cdot \frac{\mathrm{d} y}{\mathrm{d} t}`

`z\cdot \frac{\mathrm{d} z}{\mathrm{d} t}=57* 19+76* 2`

`\frac{\mathrm{d} z}{\mathrm{d} t}=(1235)/(95)=13 ft/s`