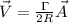Answer:
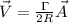
Step-by-step explanation:
We define our values according to the text,
R= Radius
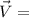 Velocity
Velocity
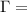 Strenght of the vortex filament
Strenght of the vortex filament
From this and in a vectorial way we express an elemental lenght of this filmaent as
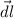 . So,
. So,
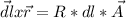
Where
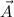 imply a vector acting perpendicular to both vectors.
imply a vector acting perpendicular to both vectors.
Applying Biot-Savart law, we have,

Substituting the preoviusly equation obtained,


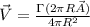
So we can express the velocity induced is,