Question

A manufacturer cuts squares from the corners of a rectangular plece of sheet metal that measures 2 inches by 7 inches (see Figure 1). The manufacturer then

folds the metal upward to make an open-topped box (see Figure 2). Letting x represent the side-lengths (in inches) of the squares, use the ALEKS graphing
calculator to find the value of x that maximizes the volume enclosed by this box. Then give the maximum volume. Round your responses to two decimal places.

Answer 1

The value of x that maximizes the volume enclosed by this box is 0.46 inches

The maximum volume is 3.02 cubic inches

Explanation:

see the attached figure to better understand the problem

we know that

The volume of the open-topped box is equal to

`V=LWH`

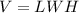
where

`L=(7-2x)\ in\\W=(2-2x)\ in\\H=x\ in`

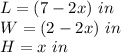
substitute

`V=(7-2x)(2-2x)x`

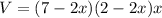
Convert to expanded form

`V=(7-2x)(2-2x)x\\V=(14-14x-4x+4x^(2))x\\V=14x-14x^2-4x^2+4x^(3)\\V=4x^(3)-18x^(2) +14x`

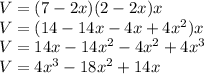
using a graphing tool

Graph the cubic equation

Remember that

The domain for x is the interval -----> (0,1)

Because

If x>1

then

the width is negative (W=2-2x)

so

The maximum is the point (0.46,3.02)

see the attached figure

therefore

The value of x that maximizes the volume enclosed by this box is 0.46 inches

The maximum volume is 3.02 cubic inches