Question

A material that has a fracture toughness of 33 MPa.m0.5 is to be made into a large panel that is 2000 mm long by 250 mm wide and 4 mm thick. If the allowable total crack length (mid crack) is 4mm, what is the maximum tensile load in the long direction that can be applied without catastrophic failure with a safety factor of 2.

Answer 1

`F_(allow) = 208.15kN`

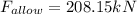
Step-by-step explanation:

The word 'nun' for thickness, I will interpret in international units, that is, mm.

We will begin by defining the intensity factor for the steel through the relationship between the safety factor and the fracture resistance of the panel.

The equation is,

`K_(allow) =(K_c)/(N)`

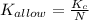
We know that
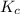`K_c` is 33Mpa*m^{0.5} and our Safety factor is 2,

`K_(allow) = (33Mpa*m^(0.5))/(2) = 16.5MPa.m^(0.5)`

Now we will need to find the average width of both the crack and the panel, these values are found by multiplying the measured values given by 1/2

For the crack;

`\alpha = 0.5*L_c = 0.5*4mm = 2mm`

For the panel

`\gamma = 0.5*W = 0.5*250mm = 125mm`

To find now the goemetry factor we need to use this equation

`\beta = \sqrt{sec((\pi\alpha)/(2\gamma))}\\\beta = \sqrt{sec((2\pi)/(2*125mm))}\\\beta = 1`

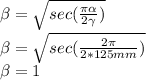
That allow us to determine the allowable nominal stress,

`\sigma_(allow) = (K_(allow))/(\beta √(\pi\alpha))`

`\sigma_(allow) = \frac{16.5}{1*\sqrt{2*10^(-3) \pi}}`

\sigma_{allow} = 208.15Mpa

So to get the force we need only to apply the equation of Force, where

`F_(allow)=\sigma_(allow)*L_c*W`

`F_(allow) = 208.15*250*4`

`F_(allow) = 208.15kN`

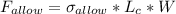
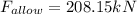
That is the maximum tensile load before a catastrophic failure.