Question

Write the point-slope form of the equation of the line through the given points through: (-3,-1) and (-2,5)?

Answer 1

The point-slope form of the equation of the line through the given points through: (-3,-1) and (-2,5) is y + 1 = 6x + 18

Solution:

Given, two points are (-3, -1) and (-2, 5)

We have to find that a line that passes through the given two points.

First let us find the slope of the line that passes through given two points.

The slope of line "m" is given as:

`\text { slope of line } m=(y_(2)-y_(1))/(x_(2)-x_(1))`

`\text { where, }\left(x_(1), y_(1)\right) \text { and }\left(x_(2), y_(2)\right) \text { are two points on line. }`

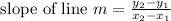
Now, let us find the line equation using point slope form

`y-y_(1)=m\left(x-x_(1)\right)`

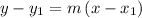
where m is slope

`\begin{array}{l}{\text { Then, line equation } \rightarrow y-(-1)=6(x-(-3))} \\\\ {\rightarrow y+1=6(x+3)} \\\\ {\rightarrow y+1=6 x+18}\end{array}`

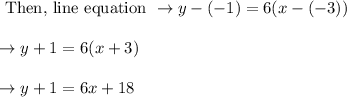
Hence the point slope form is y + 1 = 6x + 18