Question

A radioactive substance decays exponentially. A scientist begins (t=0) with 200 milligrams of a radioactive substance, where the variable t t represents time (in hours). After 24 hours, 100 mg of the substance remain. How many milligrams will remain at t= 37 hours?

Answer 1

34.35 mg.

Explanation:

We have been given that a radioactive substance decays exponentially. A scientist begins (t=0) with 200 milligrams of a radioactive substance, where the variable t represents time (in hours). After 24 hours, 100 mg of the substance remain.

We know that an exponential decay function is in form
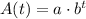`A(t)=a\cdot b^t`, where,

A(t) = Final amount,

a = Initial value,

b = Decay rate,

t = time.

For our problem initial value (a) is 200, final amount is 100 and time is 24.

`100=200\cdot b^(24)`

Let us solve for b.

`(100)/(200)=(200\cdot b^(24))/(200)`

`0.5=b^(24)`

`b=0.5^{(1)/(24)}`

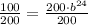
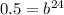
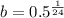
So our required function is
`A(t)=100* 0.5^{(1)/(24)*t}`.

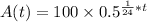Substitute
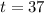`t=37` in above equation:

`A(37)=100* 0.5^{(1)/(24)*37}`

`A(37)=100* 0.5^{(37)/(24)}`

`A(37)=100* 0.3434884118645223`

`A(37)=34.34884118645223`

`A(37)\approx 34.35`

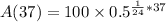
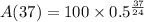
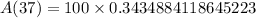
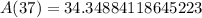
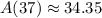
Therefore, 34.35 milligrams of substance will remain after 37 hours.