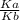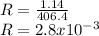Question

A 6.99-g bullet is moving horizontally with a velocity of +341 m/s, where the sign + indicates that it is moving to the right (see part a of the drawing). The bullet is approaching two blocks resting on a horizontal frictionless surface. Air resistance is negligible. The bullet passes completely through the first block (an inelastic collision) and embeds itself in the second one, as indicated in part b. Note that both blocks are moving after the collision with the bullet. The mass of the first block is 1202 g, and its velocity is +0.554 m/s after the bullet passes through it. The mass of the second block is 1523 g. (a) What is the velocity of the second block after the bullet imbeds itself? (b) Find the ratio of the total kinetic energy after the collision to that before the collision.

Answer 1

a). 1.218 m/s

b). R=2.8
`^(-3)`

Step-by-step explanation:

`m_(bullet)=6.99g*(1kg)/(1000g)=6.99x10^(-3)kg`

`v_(bullet)=341(m)/(s)`

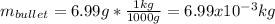
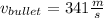
Momentum of the motion the first part of the motion have a momentum that is:

`P_(1)=m_(bullet)*v_(bullet)`

`P_(1)=6.99x10^(-3)kg*341(m)/(s) \\P_(1)=2.3529`

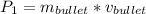
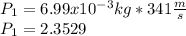
The final momentum is the motion before the action so:

a).

`P_(2)=m_(b1)*v_(fbullet)+(m_(b2)+m_(bullet))*v_(f)}`

`P_(2)=1.202 kg*0.554(m)/(s)+(1.523kg+6.99x10^(-3)kg)*v_(f)`

`P_(1)=P_(2)`

`2.529=0.665+(1.5299)*v_(f)\\v_(f)=(1.864)/(1.5299)\\v_(f)=1.218 (m)/(s)`

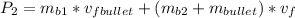
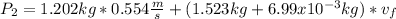
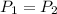
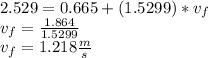
b).

kinetic energy

`K=(1)/(2)*m*(v)^(2)`

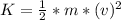
Kinetic energy after

`Ka=(1)/(2)*1.202*(0.554)^(2)+(1)/(2)*1.523*(1.218)^(2)\\Ka=1.142 J`

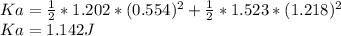
Kinetic energy before

`Kb=(1)/(2)*mb*(vf)^(2)\\Kb=(1)/(2)*6.99x10^(-3)kg*(341)^(2)\\Kb=406.4J`

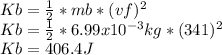
Ratio =
`(Ka)/(Kb)`

`R=(1.14)/(406.4)\\R=2.8x10^(-3)`