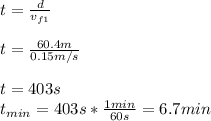Question

A(n) 69.8 kg astronaut becomes separated from the shuttle, while on a space walk. She finds herself 60.4 m away from the shuttle and moving with zero speed relative to the shuttle. She has a(n) 0.886 kg camera in her hand and decides to get back to the shuttle by throwing the camera at a speed of 12 m/s in the direction away from the shuttle. How long will it take for her to reach the shuttle? Answer in minutes. Answer in units of min.

Answer 1

The time taken is 6.7 min

Step-by-step explanation:

Using the linear momentum conservation theorem, we have:

`m_1*v_(o1)+m_2*v_(o2)=m_1*v_(f1)+m_2*v_(f2)`

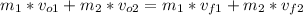
when she was 60.4m from the shuttle, she has zero speed, so the initial velocity is zero.

`m_1*0+m_2*0=m_1*v_(f1)+m_2*v_(f2)\\m_1*_(f1)=-m_2*v_(f2)\\v_(f1)=-(m_2*v_(f2))/(m_1)\\\\v_(f1)=-(0.886kg*12m/s)/(69.8kg)\\\\V_(f1)=-0.15m/s`

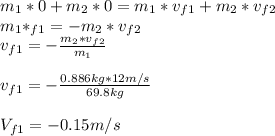
That is 0.15m/s in the opposite direction of the camera.

the time taken to get to the shuttle is given by:

`t=(d)/(v_(f1))\\\\t=(60.4m)/(0.15m/s)\\\\t=403s\\t_(min)=403s*(1min)/(60s)=6.7min`