Answer:
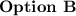
Explanation:
To solve this question we will go by the options, Let us start by substituting the point the graph passes through.
(i)
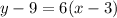
We will Substitute the point
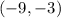 to check if it satisfies the equation. Since, it does not we will move to the second equation.
to check if it satisfies the equation. Since, it does not we will move to the second equation.
We repeat this for the remaining three options.
For (iv)
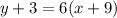
substitute
 and
and
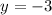
We get
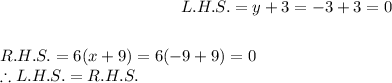
Now to verify for the slope, we rewrite the equation in the standard form
 where
where
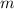 is the slope of the given equation.
is the slope of the given equation.
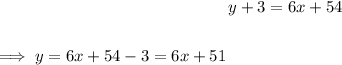
Comparing it with the standard form, we get the slope of the line to be equal to 6. Hence, Option 4 would be the correct answer.