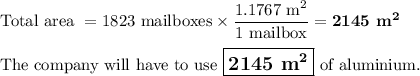Question

A company manufactures aluminum mailboxes in the shape of a box with a half-cylinder top. The company will make 1823 mailboxes this week. If each mailbox has dimensions as shown in the figure below how many square meters of aluminum will be needed to make these mailboxes? In your calculations, use the value of 3.14 for pie, and round up your answer to the next square meter.

Answer 1

2148 m²

Total Area:

Total area of the mailbox is:

Area of the cylindrical shape plus the area of the cuboid shape ( A₁ + A₂)

The area of the cylindrical shape A₁ is:

the area of top + area of the bottom

plus lateral area

The radius of the semicircle is 0.3/2 = 0.15 m

Area of top + bottom = (2)×π×(0.15)²/2 = (2)×(3.14)×(0.15)²/2= 0.07065 m²

Lateral area = π*(0.15)*L = π×(0.15)×0.55 = 0.25905 m²

A₁ = 0.07065 + 0.25905

A₁ = 0.3297 m²

Now for the cuboid

Bottom : 0.3×0,55 = 0.165 m²

Larger sides = 0.4×0,55×2 = 0.44 m²

shorter sides = 0.3×0.4×2 = 0.24 m²

A₂ = 0.165 + 0.44 + 0.24

A₂ = 0.845 m²

Then total area of 1 mailbox is : A₁ + A₂ = 0.3297 + 0.845

Ab = 1.1747 m²

And 1823 mailboxes will requiere 1.1747×1823

A = 2141,47

A = 2148 m²

Answer 2

`\large \boxed{\text{2145 m}^(2)}`

Explanation:

The area of one mailbox = the area of a rectangular box - the top of the box plus half the area of a cylinder.

SA = SA(box) - SA(top) + ½SA(cylinder)

1. Surface area of box

The formula for the surface area of a rectangular box is

SA = 2(lw + lh + wh)

Data:

l = 0.55 m

w = 0.3 m

h = 0.4 m

Calculations:

2(Top + Bottom = 2lw = 2 × 0.55 × 0.3 = 0.33 m²

2(Left + Right) = 2wh = 2 × 0.55 × 0.4 = 0.44 m²

2(Front + Back) = 2lh = 2 × 0.3 × 0.4 = 0.24 m²

Total area = 1.01 m²

2. Surface area of cylinder

The formula for the surface area of a cylinder is

SA = A(top) + A (base) + A(side) = 2A(base) + A(side)

Data:

d = 0.3 m

h = 0.55 m

Calculations:

r = ½d = ½ × 0.3 = 0.15 m

`\begin{array}{rcl}SA & = & 2\pi r^(2)+ 2\pi rh \\& = & 2 * 3. 14* 0.15^(2) +2* 3. 14 * 0.15* 0.55\\& = & 6.28* 0.0225 + 0.5181\\& = & 0.1413 + 0.5181\\& = & \mathbf{0.6594} \textbf{ m}^{\mathbf{2}}\\\end{array}`

3. Excluded area

1 top = ½ × 0.33 m² = 0.165 m²

½ cylinder = ½ × 0.6594 m² = 0.3297 m²

Total excluded = 0.4947 m²

4. Surface area of 1 mailbox

SA = (1.01 + 0.6594 - 0.4927) m² = 1.1767 m²

5. Total area of 1823 mailboxes

`\text{Total area } = \text{1823 mailboxes} * \frac{\text{1.1767 m}^(2)}{\text{1 mailbox}} = \textbf{2145 m}^{\mathbf{2}}\\\\\text{The company will have to use $\large \boxed{\textbf{2145 m}^{\mathbf{2}}}$ of aluminium.}`