Question

Fill in the blanks of the equation from the

given information.
The slope of the line is -3 and
goes through the point (13, 4).

Answer 1

We conclude that the line of equation containing the point (13, 4) with the slope m =-3 will be:

• 
  `y=-3x+43`

The graph of the line is also attached.

Explanation:

Given

• The slope of the line = m = -3

• The point = (13, 4)

Using the point-slope form of the line equation

`y-y_1=m\left(x-x_1\right)`

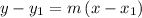
where

• m is the slope of the line

• (x₁, y₁) is the point

substituting the values m = -3 and the point (13, 4)

`y-y_1=m\left(x-x_1\right)`

`y - 4 = -3(x-13)`

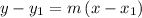
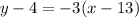
Add 4 to both sides

`y-4+4=-3\left(x-13\right)+4`

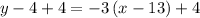
Simplify

`y=-3x+43`

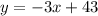
Therefore, we conclude that the line of equation containing the point (13, 4) with the slope m =-3 will be:

• 
  `y=-3x+43`

The graph of the line is also attached.