Question

Initially 5 grams of salt are dissolved in 20 liters of water. Brine with concentration of salt 2 grams of salt per liter is added at a rate of 3 liters a minute. The tank is mixed well and is drained at 3 liters a minute. How long does the process have to continue until there are 20 grams of salt in the tank?

Answer 1

3.731 minutes

Step-by-step explanation:

Let the amount of salt in the tank at any time be x(t)

Since x(0)=5 g is dissolved in 20 liters of water

Brine with 2 grams per liter salt enters the tank at the rate of 3 liters/min

Salt entering per minute is 2* 3=6 grams/min

Volume of liquid leaving the tank is the same as the volume of liquid of tank entering, 3 liters/min

volume of liquid remains at 20 liters at all times

At any given points of time, the concentration of salt is
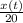`(x(t))/(20)` grams/liter

Amount of liquid leaving per minute is 3 liters/min so that the amount of salt leaving is
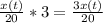`(x(t))/(20)* 3=(3x(t))/(20)` grams/minute

Differential equation governing the salt amount in the tank is

`(dx(t))/(dt)=6-(3x(t))/(20)`

Therefore,
`(dx(t))/(dt)+(3x(t))/(20)=6`

Integrating factor is
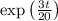`\exp\left((3t)/(20) \right )` and so the equation becomes

`(d)/(dt)\left[\exp\left((3t)/(20) \right )x(t) \right ]=6\exp\left((3t)/(20) \right )`

Therefore,
`\left[\exp\left((3t)/(20) \right )x(t) \right ]=\int 6\exp\left((3t)/(20) \right )=40\exp\left((3t)/(20) \right )+C`

`x(t)=40+C\exp\left ( -(3t)/(20) \right )`

Using the initial condition
`x(0)=5\Rightarrow C=-35`

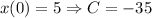
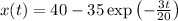`x(t)=40-35\exp\left ( -(3t)/(20) \right )` is the amount of salt at any point of time

`x(t)=40-35\exp\left ( -(3t)/(20) \right )=20\Rightarrow 35\exp\left ( -(3t)/(20) \right )=20`

`\exp\left ( -(3t)/(20) \right )=(20)/(35)\Rightarrow -(3t)/(20)=\ln\left((20)/(35)\right ) \approx -0.559616`

`t \approx 0.559616* (20)/(3)\approx 3.730733`

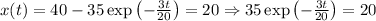
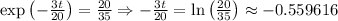
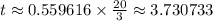
After approximately 3.731 minutes, we have 20 grams of salt in the tank