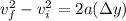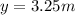Answer:
Part a)
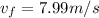
Part b)
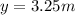
Step-by-step explanation:
Part a)
Since the diver is moving under gravity
so here its acceleration due to gravity will be uniform throughout the motion
so here we will have

here we have
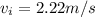
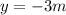
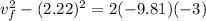
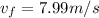
Part b)
at highest point of his motion the final speed will be zero
so we will have