Answer:
The answer is
a) 2,128 miles per gallon at 40,36 miles per hour
b) 1,388 miles per gallon at 60 miles per hour
Explanation:
Let's find the extreme points of M(x) for 30≤x≤60. M(x) simplified by dividing to 7.8.
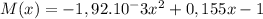
To find extreme points we find tangent of M(x) and equal it to 0.
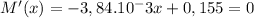
therefore x=
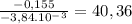
This divides our x to 2 different range 30≤x≤40,36 and 40,36≤x≤60
Now we pick a number and investigate from the ranges
30≤x≤40,36 → x = 35 → M'(35) = 0,0206 which is > 0 and that means M is increasing
40,36≤x≤60 → x = 45 → M'(45) = -0,0178 which is < 0 and that means M is decreasing
Next let's look at critical points
x M(x) Before After Decision
30 1,922 - ↑ Local Minimum Point
40,36 2,128 ↑ ↓ Local Maximum Point
60 1,388 ↓ - Local Minimum Point
As we can see (30, 1,922) and (60, 1,388) are local minimum points and (40,36 , 2,128) is the local maximum point.
Since (60 , 1,388) is the lowest local minimum point it is the absolute minimum point and (40,36 , 2,128) is the absolute maximum point.