Question

Please help!!!!!

In an isosceles triangle, the base angles are equal and the vertex angle is 80°. Find the measure of the base angles. (Note: the angles of a triangle add up to 180°.)

This is Multi step equations.

Answer 1

The measure of base angles of isosceles triangle having vertex angle as 80 degree is 50 degree each

Solution:

Given that,

In an isosceles triangle, the base angles are equal

Measure of vertex angle =
`=80^(\circ)`

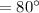
Need to calculate two equal base angle of triangle

Lets measure of each of the base angle =
`=x^(\circ)`

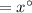
So measured of three angles of triangle are
`\mathrm{x}^(\circ) \text { and } \mathrm{x}^(\circ) \text { and } 80^(\circ)`

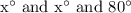
And as the angles of a triangle add up to 180°

=> x+ x + 80 = 180

On solving above expression for x we get,

`\begin{array}{l}{\Rightarrow 2 x+80=180} \\\\ {\Rightarrow 2x=180-80=100} \\\\ {\Rightarrow x=(100)/(2)=50}\end{array}`

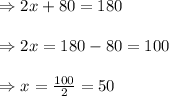
Measure of base angle = x = 50 degree

Hence measure of base angles of isosceles triangle having vertex angle as 80 degree is 50 degree each