For this case we propose a system of equations:
x: Let the variable representing the cost of a pencil
y: Let the variable representing the cost of an eraser

We substitute the first equation in the second one:
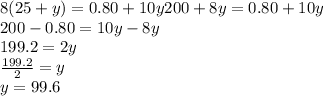
Thus, the cost of an eraser is 99.6 cents.
On the other hand:
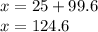
Thus, the cost of a pencil is 124.6 cents.
Answer:
The cost of an eraser is 99.6 cents.
The cost of a pencil is 124.6 cents.