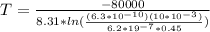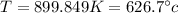Answer:
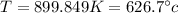
Step-by-step explanation:
We need to use Fick's Law to resolve this problem.
We know for this Law that:
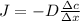
And we know as well that the diffusivity coefficient can be expressed as follows,
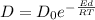
Where J is the flux of atoms, D is the diffusivity, R is the gas constant, Ed is the activation energy and \frac{\Delta c}{\Delta x} is the concentration of gradient.
To calculate the temperature we need to remplace the equation of diffusivity coefficient in the Fick's law equation.

Rearrange the equation to get the value of temperature

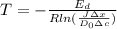
We have all the values,
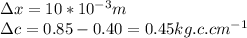

So substituting,